A Classic Genetic Model of Sexual Selection (Part I)

Background
An anthropologist friend of mine runs an online book club, where we were going through Robert Trivers' book Natural Selection and Social Theory (also available for free here), which is a collection of some of his papers with interesting and often humorous details thrown in as a preface to each chapter. Trivers was one of the greats who came out of the 1970s sociobiology wave, and I obviously recommend that book as well as any other one by him.
The book includes a paper Trivers co-authored with Jon Seger that makes a mathematical argument that females ought to chose genes benefiting their daughters first, even if it entails some expense to their male offspring. Trivers had a knack for framing his theories in terms of conflict (he coined the term “parent-offspring conflict”), and this was a case of a conflict between male and female genes. While trying to understand the mathematical details (developed mostly by Seger), I have descended into the rabbit hole that is two-locus model of sexual selection. The topic had long fascinated me, so I thought it would be a good exercise to understand the paper and then write about it.
In the “good genes for daughters” paper, Seger relies on his previous work where he extends Mark Kirkpatrick's model to allow slightly more realistic lek-like mating. In fact, it is that previous paper by Seger that will be the subject of today's post, though the reasoning is equally applicable to the better-cited one by Kirkpatrick. I like Seger's presentation of Kirkpatrick's model because it is more straightforward, and because, in my opinion, he hits on something important with his focus on lek-like mating. I will also make use of Chapter 2 of Sean H. Rice's book on evolutionary modeling. You can download the Mathematica notebooks I made while writing this post from this repository.
Seger's Paper
Historical Notes
Seger builds on Kirkpatrick's model which, along with Lande's, was hailed as a breakthrough in a long-running argument, started in 1930 by R. A. Fisher, on whether sexual selection can become a runaway process that would drive evolution of arbitrary ornaments on males without regard to individual fitness (which, in extreme cases, would be to the decrement of the population). Fisher had conjectured that it can but did not provide a proof. Fifty years later, the proponents of “good genes” hypotheses (of which Hamilton-Zuk parasite hypothesis and Zahavi's handicap principle are probably the most famous) argued that adaptationist natural selection should prevail. Lande's and Kirkpatrick's models proved Fisher correct, showing that the “decadent” runaway process can indeed occur, but without disproving any of the competing hypotheses, which may well also describe real evolutionary forces.
Further developments of Kirkpatrick's model yielded mixed results: for example, cost of female choice disrupts the runaway process, while adding mutation effects to preference locus collapses the continuous line of equilibrium into a single point. On the other hand, vertical cultural transmission was shown to reinforce the Lande-Fisher process. In summary, although we know today that Fisherian runaways are theoretically possible, questions remain how much of the diversity in secondary sexual characteristics among various species is due to this particular process. In the light of this, Seger's modeling of lek mating is interesting because, intuitively speaking, leks ought to reduce the cost of choosing a mate for females.
Basic Model
Assume we're dealing with a haploid organism (for any non-biologist reading this: haploids carry one strand of DNA while diploids carry two, one from each parent). There are two genes, $T$ (“trait”) that is only expressed in males and $P$ (“preference”) that is only expressed in females (though both sexes carry them). The $T_2$ allele (gene variant) gives males a fancy ornament which appeals to $P_2$ females but not to $P_1$ females who disregard it. Importantly, the $T_2$ allele also decreases male survival by a fraction $s$. All females have equal survival rate, regardless of genotype.
I will label the allele frequencies in the population with the respective lowercase letters. It's clear that $t_1 = 1 - t_2$ and $p_1 = 1 - p_2$. $\def\sp{^}$Let $t_2\sp{m}$ be the fraction of $T_2$ males after selection (i.e. ones that survive to maturity). Then,
$$\begin{eqnarray} t_1\sp{m} &=& t_1 ⁄ M \tag{1a} \\ t_2\sp{m} &=& (1 - s) t_2 ⁄ M, \tag{1b} \end{eqnarray}$$
where $M = t_1 + (1 - s) t_2$ is the average male viability.
Let's consider how many of the offspring will carry the $T_2$ allele. From Hardy-Weinberg rule, it should be clear that we need to take the frequency of genetically homogeneous mating pairs and add to it one half the frequency of heterogeneous pairs (the latter have 50% chance of producing offspring carrying $T_2$ in this haploid model). Note that this is the same as summing frequencies of all pairs with $T_2$ allele counted separately for each sex and dividing by two (the homogeneous pairs will be counted twice). Thus, the expected frequencies of $T_1$ and $T_2$ in the next generation are:
$$\begin{eqnarray} t_1' &=& (t_1\sp{m} p_1 + U_{21} p_2 + t_1) ⁄ 2 \label{rec-t1}\tag{2a} \\ t_2' &=& (t_2\sp{m} p_1 + U_{22} p_2 + t_2) ⁄ 2, \label{rec-t2}\tag{2b} \end{eqnarray}$$
where $U_{21}$ and $U_{22}$ are the fractions of $P_2$ females that mate with $T_1$ and $T_2$ males, respectively. Since $P_1$ females mate randomly, the fraction of $P_1$ females that mate with $T_2$ males is equal to $t_2\sp{m}$, which is the fraction of males that carry $T_2$ allele. Also note that because female survival does not depend on allele, the frequency of $T_2$ females that mate is simply $t_2$. One can also derive these equations more formally using a mating table which I describe in a section below.
Now Seger does not actually calculate the overall frequencies of $T_1$ and $T_2$ in the next generation—instead, he calculates the reproductive successes of males, labeling them $V_1$ and $V_2$. This results in exactly the same equilibrium lines, but produces wrong fitness estimates outside the equilibrium. I thought it would be interesting to look at relative fitness of $T_2$ outside the equilibrium both because the equilibrium may not always be stable and because the precise coordinates of the equilibrium are unlikely to hold in the real world where there are many evolutionary forces acting simultaneously.
Female Choice
I haven't given precise definitions of $U_{21}$ and $U_{22}$ yet because they depend on the model we're about to study. Kirkpatrick's model assumes that $P_2$ females mate at random except they prefer $T_2$ males (relative to $T_1$) by a factor $a_2$. This gives the following equations:
$$\begin{eqnarray} U_{21} &=& t_1\sp{m} ⁄ (t_1\sp{m} + a_2 t_2\sp{m}) \tag{3a} \\ U_{22} &=& a_2 t_2\sp{m} ⁄ (t_1\sp{m} + a_2 t_2\sp{m}). \tag{3b} \end{eqnarray}$$
Seger notes that Kirkpatrick's model implies female preference is independent of the relative frequencies of the two types of males, something that seems unlikely in the real world—unless the $T_2$ trait gives “an enhancement of the ‘apparency’” to the males carrying it, for example long-distance vocalization that works on $P_2$ females but not on $P_1$. In reality, a choosy female would probably continue sampling males for a longer time than a non-choosy one, especially if $T_2$ males are rare.
To account for this problem, Seger introduces a “best-of-N” model where males congregate in groups (leks) of size $N$ and females have to choose just one of the males from each lek. He reasons as follows: Suppose two types of males, $p$ and $q$, are found in leks of two. Then there will be three types of leks with frequencies ${{p\sp{2},\ 2 p q,\ q\sp{2}}}$. A female that mates randomly will choose $p$ males at a frequency $p\sp{2} + pq =$ $p(p + q) = p$. A female that always prefers $p$ males when given a choice will choose $p$ males at a frequency $1 - q\sp{2} =$ $1 - (1-p)q$ $= 1 - q + pq$ $= p + pq$. Seger then adds a factor $c$ before the $pq$ term which given $c=0$ implies fully random mating, and given $c=1$ implies exclusive preference towards $p$ males. Re-labeling $p$ to $t_2\sp{m}$ and $q$ to $t_1\sp{m}$, we get the following:
$$\begin{eqnarray} U_{21} &=& t_1\sp{m} - c t_1\sp{m} t_2\sp{m} \tag{4a} \\ U_{22} &=& t_2\sp{m} + c t_1\sp{m} t_2\sp{m}. \tag{4b} \end{eqnarray}$$
For leks of size greater than two, we simplify things by assuming $c=1$. Then,
$$\begin{eqnarray} U_{21} &=& t_1\sp{m N} \tag{5a} \\ U_{22} &=& 1 - t_1\sp{m N}. \tag{5b} \end{eqnarray}$$
Fitness Equilibria
We are now ready to calculate the allele fitness and compare our results with Seger's. The fitness equations for the two trait alleles are simply their frequencies in generation $n+1$ divided by their frequencies in the previous generation $n$:
$$\begin{eqnarray} W_{1} &=& t'_1 ⁄ t_1 \tag{6a} \\ W_{2} &=& t'_2 ⁄ t_2. \tag{6b} \end{eqnarray}$$
Plugging equations 1, 2, and 3 (for Kirkpatrick's random mating model) or 1, 2, and 4 (for Seger's best-of-two model), setting $W_1 = W_2$ and solving for $p_2$ gives the equilibrium equation (contour of equal fitness). I plotted it in Mathematica for different values of $a_2$ and $c$ respectively and got the following:

The left pane shows Kirkpatrick's model, and the right pane shows Seger's model. This exactly corresponds to figures 1a and 2a in the paper. Seger makes an additional plot where he sets $p_2 = 0.5$ and shows fitness $W$ as a function of $t_2$, the frequency of ornamented males:

The conclusion Seger draws here is that Kirkpatrick's model (left pane) results in a stable equilibrium. It's easy to see why: if $W_2 > W_1$, then $t_2$ will increase until the population ends up at the point where the two curves cross. On the other hand, if $W_1 > W_2$, then $t_2$ will decrease until, again, the equilibrium point is reached. Precisely the opposite applies to the right-side pane (best-of-two model), hence it corresponds to an unstable (divergent) equilibrium.
Fitness Landscapes
I wasn't completely satisfied with the boring-looking equilibrium lines and decided to make a plot that Seger didn't make. Specifically, I wanted a contoured density plot that would show relative fitness of $T_2$ allele with respect to $T_1$. Unfortunately, Mathematica does not provide an easy way to make a nice exportable graphic out of this type of plot, so I had to steal code from Jens Nöckel's page.

The left pane shows Kirkpatrick's model with $a_2 = 3$ ($P_2$ females mate randomly but have a $3\times$ preference bias towards $T_2$ males), and the right pane shows Seger's best-of-two model with $c = 1$ ($P_2$ females always prefer $T_2$ males when given a choice). In both cases, $s = 0.4$ (the survival rate of the ornamented $T_2$ males is 60% that of the plain $T_1$ males). The arrows show the approximate trajectories of evolution. At a certain critical frequency of choosy $P_2$ females in the population, the runaway sexual selection (red) overcomes natural selection (blue). The arrows are not perfectly horizontal because there is gamete-level correlation between the frequency of males expressing the trait and the frequency of females that prefer it (I explain this in a following section). The color represents log relative-fitness (calculated as $log[W_2⁄W_1]$), with red meaning that $T_2$ allele is winning while blue meaning that $T_1$ allele is winning. The dashed lines are simply contours with equal level of relative fitness. The thick black line is the fitness equilibrium.
Finally, I wanted to make a plot for leks of sizes greater than two. While very large leks are rare in nature, most have more than two males in them!

The left pane corresponds to leks of size $N = 3$, and the right one to $N = 6$. The equilibrium had shifted significantly, and it's no longer a straight line. The important thing to note here is just how strong Lande-Fisher runaway effect can be in large leks assuming the frequency of trait-preferring females exceeds the equilibrium threshold.
Numerical Results
The nature of runaway process appears to imply that the frequency of females exhibiting stronger trait preference should increase together with the frequency of males carrying the trait. To evaluate exactly the degree of correlation between the two is not easy, however, because of the complexity of the calculation. Fortunately, it can be estimated by numerically solving three difference equations: trait, preference, and covariance between the two. Seger's paper does not show results of the numerical calculations (except in the context of stability analysis), but Kirkpatrick's one does.
We begin by building a table that lets us predict the frequency of various allele combinations among the offspring:

Here, $x_{11}$ stands for frequency of the $T_1 P_1$ haplotype in the parent generation. The $r$ variable is the degree of recombination between the trait and preference loci (zero means the loci never recombine, while one means they always recombine). I will assume that $r = 0.5$, that is the trait and the preference genes are on different chromosomes. The remaining variables should be familiar. Seger and Kirkpatrick give a slightly different-looking table, but I prefer the format used in Sean H. Rice's book as it is more clear, in my opinion.
By multiplying the haplotype columns that include the allele of interest by the frequency column and then summing the result, we can obtain recurrence expressions for $t'_2$, $p'_2$, and $D'$, where $D = x_{11} - t_1 p_1$, i.e. the deviation between the naively expected genotype frequency and the actual one ($D$ is also called linkage disequilibrium). The expression for $t'_2$ is the same as in Equation $\ref{rec-t2}$. The expressions for $p'_2$ and especially $D'$ are more complicated. Luckily, Mathematica can handle this complexity. We can then plug the three expressions into RecurrenceTable, set the initial values for the three variables, and solve the system numerically. Repeating this process for different initial values of $p_2$ and $t_2$ lets us construct the following figure:
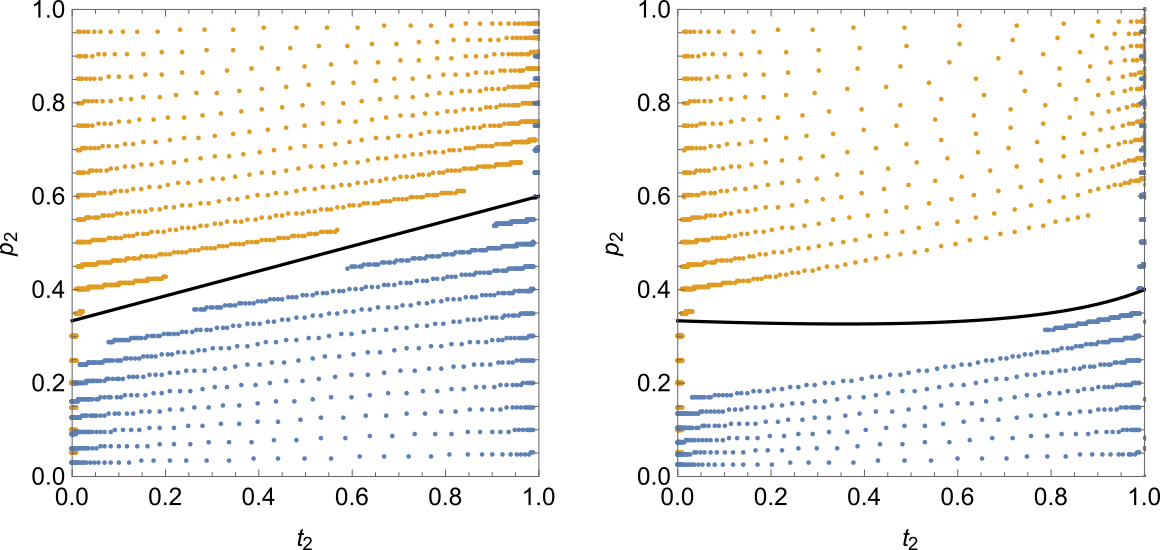
The left pane is the (familiar by now) Kirkpatrick model, and the right pane is Seger's model with $N = 3$. Each dot corresponds to one generation, so the greater the distance between the dots, the faster the evolution. The orange trace sequences begin on the left-hand side and “evolve” to the right, while the blue sequences begin on the right-hand side and “evolve” to the left. Note the slowdown of evolution near the stable equilibrium in the left pane. Also note that while correlation between trait and preference exists, it is not very strong (the slope of the trace sequences is fairly small).
Last Words
The main lesson I draw from this analysis is the somewhat obvious one: Lande-Fisher runaway process is a stronger force with lek-style mating, and it is particularly strong in large leks. For a vivid example of mating with lek size of two, see this video showing this behavior in the greater bird-of-paradise.
This concludes my exploration of Seger's paper. In a next episode, I will talk either about the Seger-Trivers “good genes for daughters” paper or about evolution of leks.